Abstract: This research dealt with observing changes which took place when subjects moved from unaided to aided decision making within two groups, A and B. A single complex problem was provided to both groups. Subjects in both groups began by using their intuition alone to prioritize alternatives. Group A then utilized AHP to re-evaluate the problem, while group B utilized Point Allocation (PA). Subjects then switched techniques to again evaluate the same decision. Subjects were provided opportunities to repeat the aided process within and among techniques and eventually converged upon a final "best" solution. That technique which, when first utilized, demonstrated the least difference or distance from the "best" solution was judged most accurate or superior for descriptive decision making. Results indicate AHP as a clearly superior technology.

1. Introduction

 Despite years of research, the question of whether descriptive decision aides contribute to unique, unstructured, and dynamic decision making remains largely unanswered. How might a decision maker determine which, if any, decision aide to utilize if each aide yields a different result, and if no yardstick exists to compare their results? A major thrust of this research was to create a sound mechanism for comparing decision technologies, and to then to test it on a complex descriptive problem. A review of past research shows a  focus largely upon the contribution of aides in "repeating" type problems, or upon utilizing normatively defined methods. (Sharda et al,1988; Vlek, 1984; Beach et al, 1988). There is continuing debate among decision theorists on the validity and reliability of utilizing decision aiding techniques and/or elements within them. Debate continues on such subjects as underlying theory (Dyer et al, 1992), weight definition (Schenkerman, 1991; Weber et al, 1988; Borcherding et al, 1991; Tversky et al, 1988; Hogarth & Einhorn, 1990;), structuring (Ravinder et al, 1988; Stillwell et al, 1987), preference expression (Cook & Kress, 1985; Creyer et al, 1990; Lindberg et al, 1989; Johnson and Payne, 1985), and scaling (Saaty, 1989; Veit, 1978; Birnbaum, 1978). 

1.1  A Variety of Decision Aiding Technologies

 It is argued that the best way to accomplish a goal of testing decision aides is to begin with a comparison of the two most dissimilar descriptive methods. If no difference in learning is perceived using these methods, it is unlikely that differences in learning will be seen using more similar methods. And if a difference is seen, then later research can focus upon individual characteristics, e.g. a focus upon scaling, while leaving the other categories constant. There are number of processes available within the descriptive class of decision making technologies (Watson & Buede, 1987). The table below presents a summary of the attributes within 4 different techniques.
 

Table 1. Characteristics of Descriptive Techniques

Characteristic	SJT	MAUT	AHP	PA
Scaling	interval; ideal and minimum acceptable	interval; utils	ratio; priorities	interval;  cognitive numeric attachment
Preference Elicitation	presentation of hypothetical cases	tradeoffs among alternatives	pairwise comparison	open, cognitive
Weighting	minimized  distance	assigned	normalized ratio via  eigenvalues	same as scale
Synthesis	regression	additive, multiplicative	additive, eigenvectors	additive, allocated weights
Structure	matrixed	matrixed or tree	hierarchial	matrixed
Built-in Feedback	synthesis	synthesis	synthesis;consistency  measure; technique  produced weightings	synthesis

SJT - social judgement theory    MAUT - multi attribute utility theory   AHP - analytic hierarchy process   PA - point allocation

Social Judgement Theory (SJT) is largely an elicitation technique, where a series of hypothetical options are presented to the decision maker. The decision maker must then apply an overall score to each hypothetical option. The weights are determined using a regression against the collected data. Finally the weights to be utilized in the selection are computed as those with minimized distance to the computed regression curve. Multiattribute Utility Theory (MAUT) is another elicitation technique where decision makers are asked to make a series of tradeoff decisions. Using the differences computed, a curve is plotted for each criterion. This curve is associated with a y axis representing UTILS, which is essentially a score, and with an x axis representing the attribute under consideration, e.g. cost, speed, reliability etc.

1.2 Two Specific Technologies

Of the techniques presented in Table 1, it was judged that PA and AHP are least alike. Differences exist within each of the characteristics. For this reason they have been selected as the techniques for comparison in this research.

1.2.1 Point Allocation

Point Allocation is a simple, and commonly used, but not well grounded approach. In PA a hypothetical number of points, e.g. 3, 5 or 10 is applied to criteria and/or alternatives. This allocation is based strictly upon a decision maker's subjective judgements. The foundations of PA are unclear, but likely grounded in the simplicity of the method. Because of its lack of theoretical grounding, it is often ignored by researchers. It is more likely to be seen in "popular" literature or in basic management texts as an example of a simple method for decision aiding (Albrecht, 1987, p 206; Van Grundy, 1988 p 244, Zeleny, 1982, p 186). For comparative purposes, researchers occasionally use variations of this technique, labeling it direct assessment (Belton, 1987; Ravinder et al, 1988; Schenkerman, 1991; Shoemaker & Waid, 1982; Saaty, 1980; Veit, 1978; Johnson & Huber, 1977). This process has been implemented in the commercial available software GroupSystems V and VisionQuest.

1.2.2 The Analytic Hierarchy Process

The Analytic Hierarchy Process (AHP)(Saaty, 1980) is a more complex, less known, but better theoretically grounded approach than point allocation. AHP utilizes pairwise comparison, hierarchial structures, and ratio scaling for applying weights to attributes. Using the technique, problems are decomposed into a hierarchy of a goal, attributes, and alternatives. Attributes / alternatives are limited to 7 on a level, following concepts espoused by Miller (1956). The fundamental synthesis technique is additive. It also has a consistency check for encouraging enforcement of judgement transitivity. The analytic hierarchy process has been well researched (Tan, 1991) and has been applied in hundreds of areas (Golden et al, 1989). The process has been implemented in the commercial software HIPRE, Criterium, and Expert Choice.

2. Experimental Design

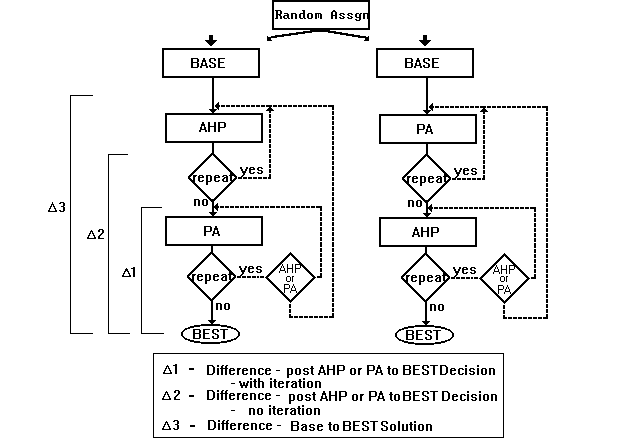
This research will observe the changes which take place when subjects move from unaided to aided decision making within two separate groups. A single complex problem, relating to a site location for the new Chicago area airport (Illinois-Indiana, 1991), is provided to both groups. Subjects must then prioritize several alternative solutions to the problem. Figure 1 depicts the research methodology, a modification of designs suggested by Brockhoff (1985) and Lai & Hopkins (1991).
 
 

Subjects begin by using their intuition alone to prioritize several alternatives. Subjects then utilize a decision aiding technique, either AHP or PA to re-evaluate the problem. The results using AHP or PA are recorded. Subjects are provided an opportunity to iterate or review and change their decision structure and values within the technique. In a normal "real world" environment where decision aides were being applied, this point is where a decision maker would stop. That is, the decision maker would accept (or possibly reject) the results produced through the technique. The research methodology in use here attempts to move the decision maker "beyond" this level, striving to move him/her closer toward an "ideal", "ground truth" decision. Toward this end, subjects switch techniques to again evaluate the same decision. That is, users of PA then use AHP, and vice versa. The use of the second technology provides another lens for analysis of the decision. While in this case subjects will be using the "other" technology, in a theoretical sense the second technology could be any other available decision technology and/or all other decision technologies. Using the second technique as an evaluation tool results are again recorded. As often as they desire, subjects are provided opportunities to repeat the aided process within and among the techniques. In an ideal environment subjects would be provided an opportunity to utilize any and all technologies available for moving them closer to an ideal decision. Eventually subjects are expected to converge upon a final "best" solution.

The "best" solution is therefore one where a) additional resources, in the form of multiple evaluations, have been applied to the problem, and b) within the limited available resources, the decision maker reaches a point where he stops and accepts one of the solutions as "best". That technique which, when first utilized, demonstrates the least difference or distance from the best solution is judged most accurate or superior.

The table below depicts the hypothetical relationships among the priorities for an individual when the data have been gathered. These hypothetical relationships are then drawn into the figure following the table.

The essential question is then, which of the points - Base, PA, or AHP is the most accurate, or lies closest to the "Best" point? Table 2 depicts the priorities derived, through the use of different decision aides, for the three example alternatives, A, B, and C. Figure 2 displays these same relationships pictorially. The points represent respectively, the results of using intuition alone (Base), the results of the initial solution produced using AHP, the results of the initial solution produced using PA, and the "best" solution that can be obtained by the subjects during the experiment. The priorities for each point, expressed as numbers between 0.0 and 1.0, represent the results of a weighted comparison of A, B, and C using each of the techniques. The di's represent euclidian distances, where the smallest d determines the technique which is closest to "best", and is therefore judged the most accurate.

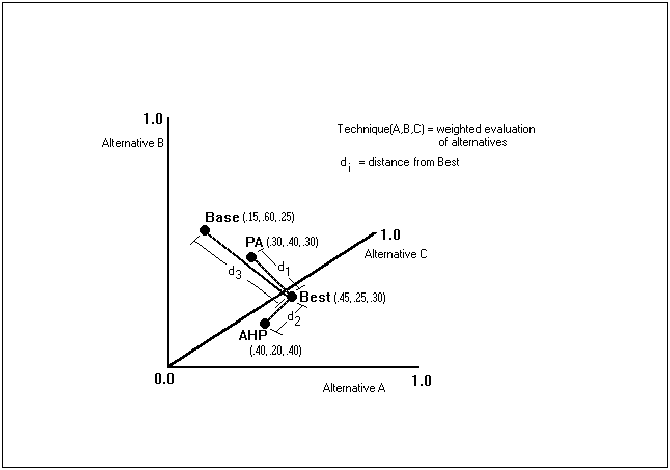
Figure 2. Distances from a "best" point for an Individual.
 

2.1 Measuring the di's, Differences, or Deltas

For statistical analysis a measure of the mean of the differences squared was utilized. The computed means then become the basis for testing hypotheses about the accuracy of the techniques. Table 3, below depicts the computation of these differences starting with AHP.

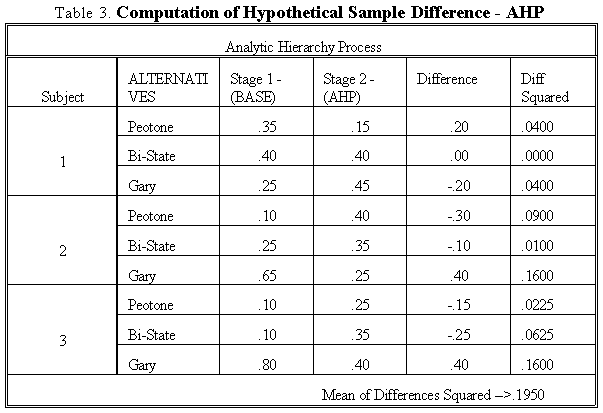
A mean of the differences squared was also then computed for individuals starting with point allocation. The difference of these sample means (µAHP-µPA) was then utilized as the statistic in the hypotheses testing.

3. Hypotheses and Results

The following hypotheses can be best understood by referencing figure 1.

3.1 Hypothesis Relating to Delta 1

The first delta, 1, depicts the difference between 1) the results from the iterated, initial use of AHP or the iterated, initial use of PA and 2) the results at BEST. That technique, AHP or PA, which produces a smaller difference is more accurate. The hypothesis to test this assertion follows:

H1: The mean of 1 for the population starting with PA is equal to the mean of 1 for the population starting with AHP.

HA: The mean of 1 for the population starting with PA is greater than the mean of 1 for the population starting with AHP.

The test statistic for this hypothesis was a t test for the differences of the means. This test yielded a t value of 2.1736 with 166 degrees of freedom and an associated probability value of .0156. This probability value is considerably smaller than the .05 pre-established for this experiment. Proper directionality is indicated. We therefore reject the null hypothesis in favor of the alternate. It can be concluded, with a 98% confidence level, that for the airport site selection decision, PA is less accurate than AHP. That is, AHP provides a greater degree of overall accuracy in decision making than that provided by PA.

3.2 Hypotheses Relating to Delta 2

The second delta, 2, represents the difference between 1) the results from the first use of AHP or PA, without iteration, and 2) the results from BEST. If this difference is less than the difference computed in delta 1, that is, with iteration, then this demonstrates the power of iterating through the process. By repeating the process, users should move more closely toward a "best" solution. The stated hypothesis is:

H2a: For the population starting with AHP, the mean of 2 is equal to the mean of 1.

HA: For the population starting with AHP, the mean of 2 is greater than the mean of 1.

For the Analytic Hierarchy Process, the test statistic for this hypothesis was a t test for the differences of the means. This test yielded a t value of 1.444 with 154 degrees of freedom and an associated probability value of .0754. This probability value is greater than the pre-established level for this experiment. We therefore fail to reject the null hypothesis at the .05 level.

A similar hypothesis would be posed for Point Allocation, i.e.,

H2b: For the population starting with PA, the mean of 2 is equal to the mean of 1.

HA: For the population starting with PA, the mean of 2 is greater than the mean of 1.

These surprising results become somewhat difficult to interpret within the context of the experiment "en mass". The directionality disagrees with the original expected results. Two related issues surround these results. First, since the bulk of the participants selected the Last AHP priorities as BEST, the differences in priorities produced by Initial versus Last PA have little bearing relative to the BEST anchor point. Second, any interpretation of "correct" movement can only be related to some "better" point. But what is the "better" point here? In retrospect, a better approach to these hypotheses may have been a two tailed test. As it now stands the null hypothesis cannot be rejected.

3.3 Hypotheses Relating to Delta 3

The third delta, 3, is equal to the difference between 1) the BASE judgements, and 2) The results of BEST. While a difference from the BASE to BEST indicates that learning has taken place, the amount of the difference should be equal for both those decision makers starting with AHP and those starting with PA. This should be true since subjects on the average will find equal opportunity, by moving among techniques irrespective of whatever technique is utilized first, to arrive at an equivalent satisfactory solution. The hypothesis is:

H3: The mean of 3 for the population starting with PA is equal to the mean of 3 for the population starting with AHP.
HA: The mean of 3 for the population starting with PA is not equal to the mean of 3 for the population starting with AHP.

The experiment yielded the following sample data.

The test statistic for this hypothesis was a two tailed t test for the differences of the means. This test yielded a t value of -.9209 with degrees of freedom of 166 and an associated probability value of .1792/2 or .0896. This probability value is greater than the .05 pre-established for this experiment. We therefore fail to reject the null hypothesis. It can be concluded therefore that for the airport site selection decision, decision movement was equivalent whether beginning with AHP or with PA. The differences or changes made by the subjects moving from their intuition only valuations to their "Best" evaluation is equivalent whether beginning with AHP or PA. These were the expected results. These results also add validity to the other hypotheses by confirming the "separate but equal" nature of the groups beginning with AHP or PA.

4. Other Results - Intra-Priority Distance

An interesting observation arose from examining the collected data. This observation looks at the collected data in a different manner - within a technique. To describe the observed pattern more clearly, I have created a metric which describes polarity in the resultant priorities. This metric provides an average of the total distance between all the resultant priorities. I have termed this metric Intra Priority Distance (IPD). As an example of how it operates imagine a decision with 3 alternatives which has derived priorities of .5, .4, and .1. This example would yield an IPD of [((.5-.4)+(.5-.1)+(.4-.1))/3] or .266. A decision where all alternatives had equal priorities would yield an IPD of zero. A decision with an infinite number of alternatives, the first with a priority of 1.0 and the all others with priorities of 0.0 would yield an IPD approaching 1.0. Therefore

(3) 0.0 <= {is less than or equal to} IPD < {is less than} 1.0.

This data provides two indications. The first is that differences exist among the techniques. The second is that intuition appears to provide larger IPDs, and that AHP follows closely behind. Do decision makers on the average produce closer priorities with closer examination of alternatives? Indications from this limited data set indicate that they do. What is the root cause of these tendencies? Since both PA and AHP use the same additive synthesis method, the differences must lie deeper within the application of values to the model. Possible explanations include the different scaling methods, particularly an ordinal interpretation when using PA and differences in the mental polarity established when performing direct assessment versus paired comparison.

The potential use of the IPD measure as a tool is seen as dependent upon a decision maker's purpose. The IPD may be useful for distinguishing those techniques which more clearly separate the prioritization of alternatives. Given the data assembled here it may also be an indicator of learning. That is a low IPD may be an indication of lack of learning. Additional research is necessary to test the validity and reliability of these indications.

5. Summary

This research has shown that, for the case under study, the Analytic Hierarchy Process is a more accurate decision making aide than Point Allocation. It has also shown that iteration for Point Allocation provides no additional accuracy. It has demonstrated that iteration within AHP may have value added but that this area deserves more in-depth study. This research has also brought forth discovery that distances between decision priorities may vary depending upon the technology in use and the stage of the decision process. This knowledge should provide decision makers with a greater awareness of the value of decision aides in the decision making process, and ultimately provide what decision makers see as better decisions.

Albrecht, Karl G. (1987). BrainPower. New York: Prentice-Hall.

Beach, Lee R., Vlek, Charles, and Wagenaar, Willem A. (1988). Models and Methods for Unique Versus Repeated Decision Making. Report of an Informal Conference Held at Leiden University, 21-23 April.

Belton, Valerie. (1987). A Comparative Study of Methods for Discrete Multiple Criteria Choice - Some Empirical Results. Working Paper, University of Kent at Canterbury, England.

Birnbaum, Michael H. (1978). Differences and Ratios in Psychological Measurement in N.John Castellan, Jr. and Restle, Frank (eds.) Cognitive Theory, vol 3. (pp. 33-74). New York: Halstead Press, Wiley & Sons

Borcherding, Katrin, Eppel, Thomas and Von Winterfeldt, Detlof. (1991). Comparison of Weighting Judgements in Multiattribute Utility Measurement. Management Science, 37, 1603-1619.

Brockhoff, Klaus, (1985). Experimental test of MCDM algorithms in a modular approach. European Journal of Operations Research, 22, 159-166.

Cook, Wade, and Kress, Moshe. (1985). Ordinal Ranking with Intensity of Preference,", Management Science, 31, 26-32.

Creyer, Elizabeth H., Bettman, James R., and Payne, John W. (1990). The Impact of Accuracy and Effort Feedback and Goals on Adaptive Decision Behavior. Journal of Behavioral Decision Making, 3, 1-16.

Dyer, J., Fishburn, P., Steuer, R., Wallenius, J., and Zionts, S. (1992). Multiple Criteria Decision Making, Multiattribute Utility Theory: The Next Ten Years. Management Science, 38, 645-654. Golden, B.L., Wasil, E.A. and Harker, P.T. (1989). The Analytic Hierarchy Process: Applications and Studies. New York, NY: Springer-Verlag.

Hogarth, Robin, and Einhorn, Hillel. (1990). Venture Theory: A Model of Decision Weights. Management Science, 36, 780-803.

Illinois-Indiana Regional Airport Site Selection Report Abstract. (1991). Chicago: TAMS Consultants, Inc.

Johnson, Eric, and Payne, John. (1985). Effort and Accuracy in Choice. Management Science, 31, 395-414.

Johnson, Edgar, and Huber, George. (1977). The Technology of Utility Assessment. IEEE Transactions on Systems, Man and Cybernetics, 7, 311-325.

Lai Shih-Kung and Hopkins, Lewis D. (1991). Can Decision Makers Express Preferences Using MAUT and AHP: An Experimental Comparison. Paper under review for IEEE Systems Man and Cybernetics. Winter.

Lindberg, Erik, Garling, Tommy, and Montgomery, Henry. (1989). Differential Predictability of Preferences and Choices. Journal of Behavioral Decision Making, 2, 205-219.

Miller, G.A.. (1956). The Magic Number Seven, Plus or Minus Two: Some Limits on our Capacity for Processing Information. Psychological Review, 63, 81-97.

Ravinder, H.V., Kleinmuntz, Don N., and Dyer, James S. The reliability of subjective probabilities obtained through decomposition. Management Science, 34, 186-199.

Saaty, Thomas L.. (1989) Decision Making, Scaling, and Number Crunching. Decision Sciences, 20, 404-409.

Saaty, Thomas L. (1980). The Analytic Hierarchy Process. New York: McGraw-Hill. Schenkerman, Stan. (1991). Use and Abuse of Weights in Multiple Objective Decision Support Models. Decision Sciences, 22, 369-378.

Schoemaker, Paul J.H., and Waid, C. Carter. (1982). An Experimental Comparison of Different Approaches to Determining Weights in Additive Utility Models. Management Science, 28, 182-196. Sharda, Ramesh, Barr, Steve H., and McDonnell, James C. (1988). Decision Support System Effectiveness: A Review and an Empirical Test. Management Science, 34, 139-159.

Stillwell, William G., Winterfeldt, Detlof Von, and John, Richard S. (1987). Comparing Hierarchial and Nonhierarchial Weighting Methods for Eliciting Multiattribute Value Models. Management Science, 33, 442-450.

Tan, Tehchu. (1991). Issues on Justification of the Analytical Hierarchy Process. Working Paper, School of Management, SUNY Buffalo, February.

Tversky, Amos, Sattath, Shmuel, and Slovic, Paul. (1988). Contingent Weighting in Judgement and Choice. Psychological Review, 95, 371-84.

Van Grundy, A.B. (1988). Techniques of Structured Problem Solving. New York: Van Nostra and Reinhold Company.

Veit, Clarice T. (1978). Ratio and Subtractive Processes in Psychophysical Judgement. Journal of Experimental Psychology, 107, 81-107.

Vlek, Charles. (1984). What Constitutes 'A Good Decision?' Acta Psychologica, 56, 5-27.

Watson, Stephen R. and Buede, Dennis M. (1987). Decision Synthesis: The Principles and Practice of Decision Analysis. New York, NY: Cambridge University Press.

Weber, M., Eisenfuhr, F., and Von Winterfeldt, D. (1988). The Effects of Splitting Attributes on Weights in Multiattribute Utility Measurement. Management Science, 34, 431-445.

Zeleny, Milan. (1982). Multiple Criteria Decision Making. New York: McGraw-Hill.

(c) 1994 Permission Granted to Use in Academic Environments