A Risk Management Methodology for Information Security: The Analytic Hierarchy Process

John H. Saunders, PhD, GSEC

Information Resources Management College,

Washington DC, 20319

saunders@ndu.edu.

 

Abstract

 

This paper addresses the use of a specific methodology termed the Analytic Hierarchy Process (AHP) for risk management. This method provides for both the analysis and synthesis of risk. It also combines both qualitative judgments and quantitative measures under a single umbrella. This technique thus provides a robust and encompassing treatment of security management issues. The bases of AHP are:

 

• The construction of hierarchies of objectives and alternatives for meeting those objectives.
• Relative pair wise comparison of problem attributes including, where necessary levels of uncertainty.
• A common scale for synthesizing results.
• A sensitivity analysis capability.

 

This well proven approach has been shown to be of significant value in the arena of Information Technology evaluation. A simple example “Establishing priorities in the area of security countermeasure investment” is presented to demonstrate its value.

 

Introduction

 

As Stephen Fried points out in his discussion of Risk Analysis Methodologies[2001],

 

“… All of these are areas of risk that can’t clearly be quantified. Quantitative analysis works great in areas with solid histories of financial or statistical models on which to base good business judgments. Unfortunately, computer security doesn’t have any of these models on which to go by.”

 

The differences between risk analysis and risk management are made clearer by Fred Cohen [1999], and Allan Micksch [2000]. The key challenge for the information security manager is to locate and utilize a methodology where the limited quantitative data that is available may be combined with the more qualitative “expert” opinion. Additionally a way of providing balance for management in the tradeoffs of comfort, cost, and feasibility is needed. There are a number of methods in this arena such as cost benefit analysis, decision trees, and decision matrices [Saunders, 1998]. The AHP is another such method, which has been shown to provide greater depth of analysis [Saunders, 1994] than the other methods and can be utilized more effectively with both quantitative and qualitative data. Its use is becoming especially important in an age when an organization must offer proof of “due diligence” in the analysis and management of security tradeoffs.

 

A Cognitive Basis for Utilizing AHP

 

 When attempting to make decisions, the temptation to quantify is ever present. It is a learned trait. At an early age we learn that 1+1=2, and that this relationship never changes. As an exact science mathematics provides a certain illusion of invulnerability and comfort. Regretfully, when we grow older we learn that life is really an essay question. There are rarely “right” answers to many of the challenges we face. And the qualitative issues are often seen as more important. The Information Security manager is faced with tradeoff decisions such as protection versus cost, security versus accessibility, and time versus information quality.

 

Faced with these types of difficult decision tradeoffs, decision makers revert to one of two flawed processes (or a combination of the two). Those processes are “BOGGSAT”, and “The Magic Number Three plus or minus two.”

 

BOGGSAT is an abbreviation for Bunch of Guys and Gals Sitting Around Talking. This is often how major decisions are made. A group vested with a decision, for example selecting an IDS vendor or establishing a security policy, convenes in a conference room. They proceed to spend hours throwing around the pros and cons of one approach versus another, rehashing old points, rarely recording the discussion or process (what process!) and surfacing old feuds. The group also typically suffers from domination by one or two outspoken (yet often also poorly uneducated in the topic) members. Somehow miraculously, 5 minutes before the conclusion of the scheduled meeting an unholy “consensus” is formed. It is unlikely that many in the meeting could tell you how they got there – they just did. And it is also unlikely that they could provide you with more than one or two sketchy reasons on why they made the decision! This brings us to the second flawed process, often used for personal decisions.

 

An understanding of The Magic Number Three Plus or Minus Two needs to stem from work done by Psychologist George A. Miller [Miller, 1956]. Dr. Miller provided a basis for demonstrating how our short term and long term memories just seem to run out of steam when attempting to remember more than 7 items. Why are there 7 numbers in a phone number? Why, when singing the 12 days of Christmas, do we forget what comes after 5 golden rings? Is it six maids a milking, six swans a swimming, or six geese a laying?

 

What makes Miller’s work perhaps even more germane is that the number seven seems to work well for only single dimension lists. But making decisions is about understanding relationships among options and requirements. This is where computational complexity comes into play, and why it’s really about the magic number three.  If you have only three items for example, yet each item can take on a 1 or a 0 state, then you have a possible combination of states equal to 2 x 2 x 2 or eight. Even small “real world” problems can produce incredible computational complexity.

 

Our natural reaction to this combinatorial complexity is to simplify. We simply throw out all but a very few number of objectives, perhaps as few as 1 or 2, at most 3, and then base our decision upon those few mentally digestible objectives. For example if we are focusing on buying a car, we throw away all but a couple of criteria, e.g. cost range and style. This simplification can and will get you into trouble much sooner than later, and is why Dr Tom Saaty, while on the faculty at the Wharton School, created a method called the Analytic Hierarchy Process [Saaty, 1990].

 

Basic Tenets of the Analytic Hierarchy Process

 

The AHP was created to overcome the decision limitations just discussed. It is a method for handling cognitive complexity and for providing a basis for eliciting, discussing, recording, and evaluating the elements of a decision. Its constructs include:

 

• Building a hierarchy of objectives/criteria and alternatives.
• Comparing – relatively – the problem attributes including, where necessary levels of uncertainty.
• Synthesizing the results using a common scale.
• Performing sensitivity analysis.

 

Each of these areas is discussed in paragraphs below.

 

Hierarchies

 

Humans are quite accomplished at creating hierarchies, both for building up new subject areas and for problem decomposition. A hierarchy provides a visual basis for understanding all the elements in a problem domain. And it allows individuals to expand the scope of a problem while still maintaining a sense of order. Creating hierarchies is an essential part of the Analytic Hierarchy Process. The diagram below pictures a sideways hierarchy for prioritizing budget items in information security. It is a very simplified example. It provides a framework for looking at the tradeoffs and conflicting objectives of keeping threats to a minimum, while also keeping the budget minimal. The issues related to how much should be allocated to each of the suggested budget countermeasure areas (Antivirus Software, IDS, and Training) include the costs, threats/threat levels, and the expected longevity of a countermeasure area.

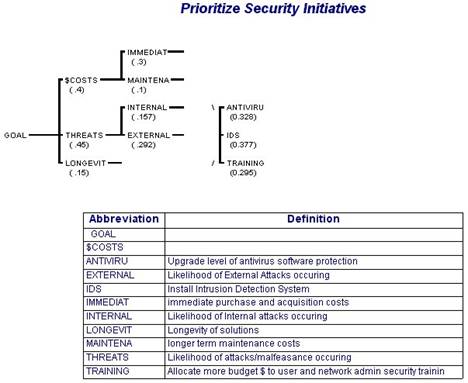
Figure 1 - Hierarchy and Definitions

 

Note that this specific model is NOT meant to be a template for any organization. It is only hypothetical. Security models must be established individually by an organization. The information security issues for a small retailer would be very different from those of a large national security organization such as NSA and should be reflected as such in the model. Another essential element of AHP is comparison.

 

Paired Comparison

 

Humans are quite accomplished at the comparison of things. While it is often difficult to exactly measure such things as political pressure or opinion on styles, we can judge these things relative to other elements of the same ilk. We can say that one objective is politically more sensitive than another, for example hiring the bosses’ son versus an off the street applicant. Or we can say that we prefer one particular style to another, say a command line environment to a windows one. Doing paired comparison is also an important part of AHP. The diagram below depicts a session where for example a manager must make a decision as to the relative value of anti-virus software versus an IDS for combating internal threats.

 

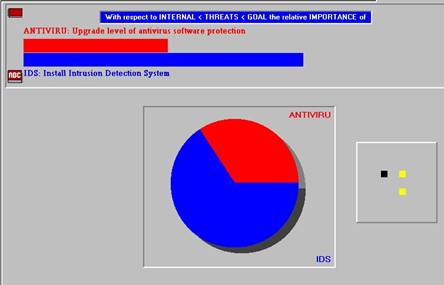
Figure 2 - Paired Comparison Example

 

Each objective would be compared against each other objective to establish their relative priorities. And each alternative would be compared against each objective to determine how well it fares. So for example while perhaps IDS is more expensive than AV software, it may also provide a measurable edge in protection.

 

Synthesis

 

Another important part of AHP is synthesis. In order for us to synthesize all the elements of a decision, we need a common basis for doing so. But what is the common basis, the common thread for cost, and performance, and style, and risk? How might you combine all these disparate elements?  Most frequently we use dollars. We boil everything down to “How much does it cost – what is the dollar value of this decision? For some things this is not difficult. For example in selecting disk storage we can use $1 a megabyte, or for processor cycles 2.5x10 ^–20 cents each, or for router parsing $1 per GB per second. But for other attributes quantification is a vexing process. How do you apply dollars to preferences on service, customer satisfaction, or the subjective probability of assuming a risk?

 

To combat this quandary, Dr. Saaty created a common numeric ratio scale mechanism. A ratio scale does not require a person to apply fixed values (e.g. dollars) to an attribute. Rather it utilizes the paired comparisons discussed above as its basis.  You likely have heard the phrase, “you cannot compare apples to oranges.” This is simply not true. Oranges are more acidic than apples, have a brighter color, and a rougher skin. A ratio scale can provide a common basis for synthesizing both strongly quantitative and qualitative variables – relatively, using ratios. So a manager or analyst would make a determination - what is the ratio of customer satisfaction of vendor A compared to vendor B? Or what is the ratio of a threat of a DDOS attack versus a Worm?

 

The mathematics utilized in Dr. Saaty’s ratio scale method to establish the eventual prioritized budget items is beyond the scope of this paper.  It utilizes supermatrices, eigenvectors, and eigenvalues to collect and provide feedback to the user in a numeric form. Consult Saaty₂, 1990 for details. His method assigns numeric values to judgments made by a user. It then multiplies and adds these results together to produce a prioritization of alternatives such as that depicted below.

 

Figure 3 - Prioritized Synthesis of Alternatives

 

The initial production of prioritized results is not a reason to accept them at face value. There should also be some insurance that the decision is "flexible", i.e. will allow for give in an uncertain world.

 

Sensitivity Analysis

 

Another large part of Dr. Saaty’s method is the concept of sensitivity analysis or “what if?” The sensitivity feature allows the model builder to play with the weights assigned to the objectives. For example what if there is some expectation that the financial state of the company will change soon? This would likely change the weight placed on Cost, one way or the other. What will then happen to the end prioritization if this weight is changed? The sensitivity feature, outlined below, provides a mechanism for helping the manager or analyst define the range of possibilities that the organization will face.

 

Figure 4 - Sensitivity Analysis

 

Utilizing this feature, the decision making group, manager, or analyst can change the importance of costs, threats or longevity, and view the proportional change in the prioritization placed upon IDS, Anti-virus or Training. It is difficult to portray this analysis in a paper, because the process is dynamic, i.e., the bars can be moved back and forth on a real time basis to view the accompanying change on the alternative priorities. The diagram below also depicts the synthesized results. So, in this example, anti-virus software scores high on the longevity criterion, but lower than both the other two criteria on cost and threat mitigation. Since the longevity criterion (yellow bar) has a lower weight, it provides little overall help to boost the importance of anti-virus software.

 

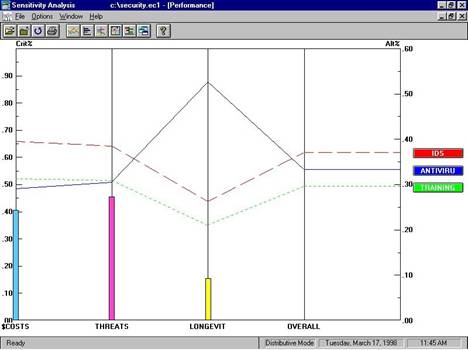
Figure 5 - Cumulative Results

 

Other Application Areas

 

The use of AHP for Risk analysis is not new. It has been applied in a wide variety of risk management applications such as air traffic control [Bachu et al, 1993], environmental risk assessment [Barnthouse, 1982; Gerrits, 1994; Walsh, 1991], energy issues [Dey,1994; Hamalainen,1992] source selection [Pierce, 1992; Vellore, 1991], National Security Risk [Toshtzar, 1988] and information technology [Ghotb, 1996;  Kitamura, 1992;  Riggs, 1994,] and especially EDP auditing [Neim, 1986;  Riley, 1987]. The basis of The Gartner Group’s “Decision DriversÔ” is also AHP.

 

AHP can also be utilized to add value to cost benefit analysis especially in the area of evaluating qualitative variables [Saaty₂, 1990]. The application of AHP is made easier by the use of software packages available form several vendors [Buede, 1992]

 

Conclusion

 

This paper has attempted to extend the general topic of risk management in the arena of Information Security. It described the tenets of applying the Analytic Hierarchy Process to risk management through a simple example.  The information security arena provides a unique and worthwhile area of investigation and application for AHP. More security professionals should consider its use in evaluating the tradeoff among alternatives in the Information Technology arena.